第1章 問題
- $a$を定数として,$x$,$y$,$z$の速度成分が
\[
u=ax, \quad v=ay,\quad w=-2az
\]
で与えられるとき,流線を求めよ.
解答
- 二次元流れにおいて,$x$,$y$方向の速度成分$u$,$v$が
\begin{align*}
u=ax+by, \quad v=cx+dy
\end{align*}
で表されるとき,次の条件を求めよ.
- $u$,$v$が連続の方程式を満足する条件
- 流れが渦なしであるための条件
ただし,$a$,$b$,$c$,$d$は定数である.
解答
-
定常な非圧縮性流れにおいて,連続の式は円筒座標$r$,$\theta$,$z$を用いて
\begin{align*}
\frac{1}{r}\frac{\partial}{\partial r}(rv_r)
+\frac{1}{r}\frac{\partial v_\theta}{\partial \theta}
+\frac{\partial v_z}{\partial z}
=0
\end{align*}
とあらわされることを導け.ここに$v_r,v_\theta,v_z$は$r,\theta,z$方向
の速度成分である.
解答
-
流線に沿った一次元のオイラーの運動方程式は,重力場において
\begin{align*}
\frac{\partial V}{\partial t}
+V\frac{\partial V}{\partial s}
=g\cos\alpha-\frac{1}{\rho}\frac{\partial p}{\partial s}
\end{align*}
とあらわされることを導け.
ここに,$s$は流線に沿って測った長さ,$t$は時間,$V$は流線に沿う速度,
$\alpha$は重力の加速度$g$と流線のなす角度である.
解答
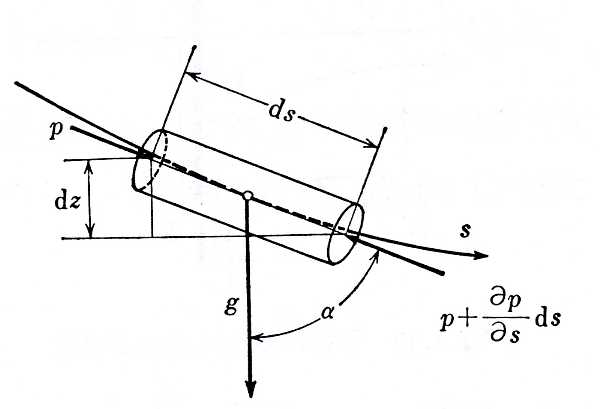 図1.14:一次元オイラー運動方程式の誘導
図1.14:一次元オイラー運動方程式の誘導
-
前問の一次元のオイラーの運動方程式を流線に沿って積分すれば,つぎの非定常
のベルヌーイの式が導かれることを示せ.ここに$z$は鉛直上方を正とする.
\begin{align*}
\frac{p}{\rho}+gz+\frac{1}{2}V^2
+\int_0^s\frac{\partial V}{\partial t}\mbox{d}s=\mbox{const.}
\end{align*}
解答
-
流体が重力場で静止状態にあるとき,高さ$z$の位置の圧力を$p^\prime$とすれ
ば,$p^\prime$と$z$との間にどのような関係式が成立するか? つぎに重力場
における流体の運動においては,圧力$p$を静止状態の値$p^\prime$から測るこ
ととし,$p-p^\prime=p^*$とおけば,ベルヌーイの式は
\begin{align*}
p^*+\frac{1}{2}\rho V^2=\mbox{const.}
\end{align*}
となり,重力の影響を形式的に除外できることを示せ.
解答
-
重力場において一定の角速度$\varOmega$で鉛直軸のまわりに回転する座標系で,
回転軸からの距離を$r$,相対速度を$V$,高さを$z$とするとき,ベルヌーイの
式は
\begin{align*}
p+\rho gz -\frac{1}{2}\rho\varOmega^2r^2+\frac{1}{2}\rho V^2
=\mbox{const.}
\end{align*}
と表されることを導け.つぎに流体が相対的静止(相対的つりあい)の状態にあ
るときの圧力を$p^\prime$とし,$p-p^\prime=p^*$とおけば,ベルヌーイの式は
\begin{align*}
p^*+\frac{1}{2}\rho V^2=\mbox{const.}
\end{align*}
となり,遠心力および重力の影響を形式的に除外できることを示せ.
解答
-
半径$r$における接線方向速度$v_\theta$がつぎの式で与えられる円運動は,渦
運動か,渦なし運動か? ただし,$k, \omega$は定数である.
解答
- 自由渦 $v_\theta=k/r$
- 強制渦(forced vortex)$v_\theta=\omega r$
-
速度$V$,直径$d$の円形断面の噴流が平板に垂直に当たるとき,平板の受ける力
$F$を求めよ.
解答
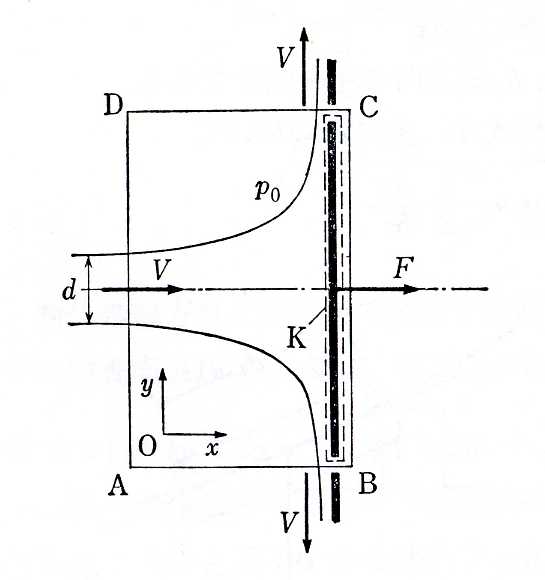 図1.15:平板に垂直に当たる噴流
図1.15:平板に垂直に当たる噴流
-
断面積$\sigma$,方向変化角度$180^\circ$の曲り管内を速度$V$で流体が流れる
とき,曲り管に働く力$F$を求めよ.ただし流体の粘性にもとづく圧力降下はな
く,管内いたるところで圧力は一定で$p$に等しいと仮定する.
解答
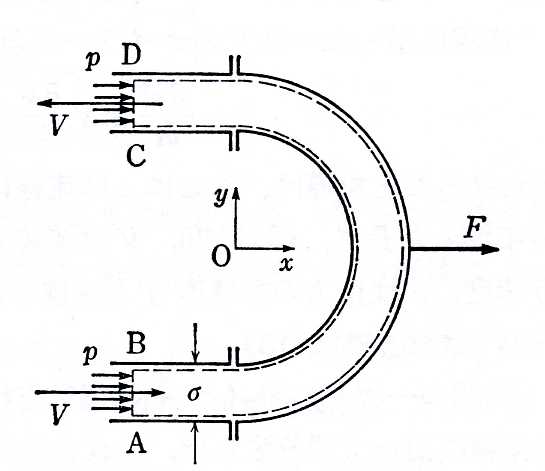 図1.16:180°曲り管
図1.16:180°曲り管





