第1章 問題4 解答

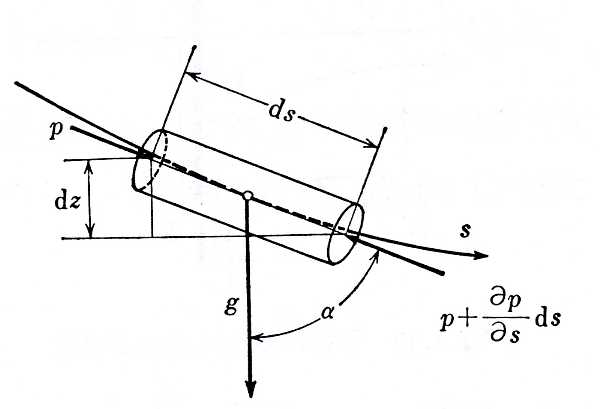図に示すように流線に沿って座標$s$をとる．ここで，流管を構成している流体の塊を考える．流体塊の重心が時刻$t$に$s$にある．流速を$V(t,s)$で表せば，この塊は$\Delta t$秒間に$V(t)\Delta t$だけ移動するので，この間の速度変化$\Delta V$は \begin{eqnarray} \Delta V&=&V(t+\Delta t,s+V(t)\Delta t)-V(t,s)\nonumber \\ &=&\frac{\partial V}{\partial t}\Delta t +V\frac{\partial V}{\partial s}\Delta t +\dots\nonumber \end{eqnarray} したがって，この流体塊の加速度$a$は \begin{equation} a=\lim_{\Delta t\rightarrow 0} \frac{\Delta V}{\Delta t} =\frac{\partial V}{\partial t}+V\frac{\partial V}{\partial s} \label{acc} \end{equation}

一方，この流体には流体塊の表面に直角内向きに作用する圧力，および流体塊の重心に重力が働く．

圧力による力の流線の方向分力を$F_p$とすれば \begin{eqnarray} F_p&=&pA-\left(p+\frac{\partial p}{\partial s}\mbox{d}s\right) \left(A+\frac{\partial A}{\partial s}\mbox{d}s\right) +\left(p+\frac{1}{2}\frac{\partial p}{\partial s}\mbox{d}s\right) \frac{\partial A} {\partial s}\mbox{d}s\dots \nonumber\\ &=&-A\frac{\partial p}{\partial s}\mbox{d}s+\dots \label{fp} \end{eqnarray} ここに，第一式の右辺第3項は流管の直径が変化するとき，流管の側面に働く力である．

流体塊に働く重力の流線方向分力$F_g$は \begin{equation} F_g=\rho \left(A+\frac{1}{2}\frac{\partial A}{\partial s}\mbox{d}s\right)\mbox{d}s \, g\, \cos \alpha \label{fg} \end{equation}

ニュートンの運動方程式より \begin{equation} \rho \left(A+\frac{1}{2}\frac{\partial A}{\partial s}\mbox{d}s\right)\mbox{d}s\, a=F_p+F_g \end{equation} 両辺を$\rho\, A\, \mbox{d}s$で割り，$\mbox{d}s\rightarrow 0$の極限をとれば，流線に沿った一次元のオイラーの運動方程式が得られる． \begin{equation} \frac{\partial V}{\partial t}+V\frac{\partial V}{\partial s} =-\frac{1}{\rho}\frac{\partial p}{\partial s}+g\cos\alpha \end{equation}

別解

テキストで求めた運動方程式(1.32)から誘導する． \begin{equation} \left. \begin{array}{rcl} \displaystyle{ \frac{\partial u}{\partial t} +u\frac{\partial u}{\partial x} +v\frac{\partial u}{\partial y} +w\frac{\partial u}{\partial z} } &=& \displaystyle{ X-\frac{1}{\rho}\frac{\partial p}{\partial x} }\tag{1.32}\label{eq:1.32}\\%[3mm] % \displaystyle{ \frac{\partial v}{\partial t} +u\frac{\partial v}{\partial x} +v\frac{\partial v}{\partial y} +w\frac{\partial v}{\partial z} } &=& \displaystyle{ Y-\frac{1}{\rho}\frac{\partial p}{\partial y} }\\%[3mm] % \displaystyle{ \frac{\partial w}{\partial t} +u\frac{\partial w}{\partial x} +v\frac{\partial w}{\partial y} +w\frac{\partial w}{\partial z} } &=& \displaystyle{ Z-\frac{1}{\rho}\frac{\partial p}{\partial z} } \end{array} \right\} \end{equation}
別解解説図
別解解説図

流れは$\, (x, z)\, $平面内の二次元流れとする．$\, x\, $軸を水平方向，$\, z\, $を鉛直上向きとすれば，外力は$\, X=0\, $，$\, Z=-g\, $となるので，運動方程式\eqref{eq:1.32}は次式で表現される． \begin{equation} \left. \begin{array}{rcl} \displaystyle{ \frac{\partial u}{\partial t} +u\frac{\partial u}{\partial x} +w\frac{\partial u}{\partial z} } &=& \displaystyle{ -\frac{1}{\rho}\frac{\partial p}{\partial x} }\label{eq:x}\\%[3mm] % \displaystyle{ \frac{\partial w}{\partial t} +u\frac{\partial w}{\partial x} +w\frac{\partial w}{\partial z} } &=& \displaystyle{ -g-\frac{1}{\rho}\frac{\partial p}{\partial z} } \end{array} \right\} \end{equation}

式\eqref{eq:x}の第1式に$\, \mbox{d}x/\mbox{d}s=\cos\theta\, $，第2式に$\, \mbox{d}z/\mbox{d}s=\sin\theta\, $を掛て両辺ごとに和をとれば \begin{equation} \left(\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+w\frac{\partial }{\partial z}\right)(u\cos\theta+w\sin\theta) =-g\sin\theta - \frac{1}{\rho}\left(\frac{\partial p}{\partial x}\frac{\mbox{d}x}{\mbox{d}s} +\frac{\partial p}{\partial z}\frac{\mbox{d}z}{\mbox{d}s} \right)\label{eq:8} \end{equation}

別解解説図を参考にして， \begin{equation} u\cos\theta+v\sin\theta=V \end{equation} 一方，$\, u\partial(\; )/\partial x+w\partial(\; )/\partial z\, $ は速度ベクトルとgradientの内積であるから，速度と流線方向の勾配積に他ならない．また，$\theta=-(\pi/2-\alpha)\, $を考慮すれば，式\eqref{eq:8}は次式のように表現される． \begin{equation} \frac{\partial V}{\partial t}+V\frac{\partial V}{\partial s} =-\frac{1}{\rho}\frac{\partial p}{\partial s}+g\cos\alpha \end{equation}