第1章 問題3 解答
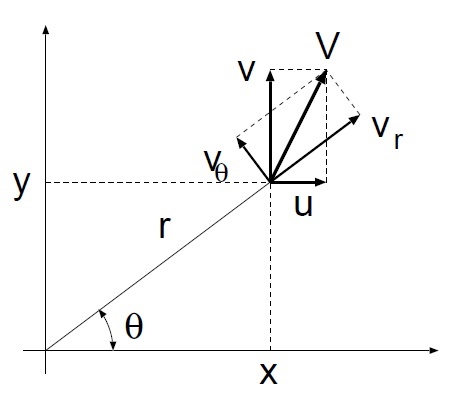直角座標と極座標の関係
\begin{equation}
x=r\cos\theta,\quad y=r\sin\theta
\end{equation}
速度の関係
\begin{equation}
u=v_r\cos\theta-v_\theta\sin\theta,\quad
v=v_r\sin\theta+v_\theta\cos\theta\label{vel-x}
\end{equation}
\begin{equation}
v_r = u\cos\theta+v\sin\theta,\quad
v_\theta=-u\sin\theta+v\cos\theta\label{vel-r}
\end{equation}
微分演算子の関係
\begin{eqnarray}
\frac{\partial}{\partial r}
&=&\frac{\partial}{\partial x}\frac{\partial x}{\partial r}
+\frac{\partial}{\partial y}\frac{\partial y}{\partial r}
=\frac{\partial}{\partial x}\cos\theta
+\frac{\partial}{\partial y}\sin\theta\label{par-r}\\
\frac{\partial}{r\partial \theta}
&=&\frac{1}{r}
\left(\frac{\partial}{\partial x}\frac{\partial x}{\partial \theta}
+\frac{\partial}{\partial y}\frac{\partial y}{\partial \theta}\right)
=\frac{1}{r}\left(\frac{\partial}{\partial x}(-r\sin\theta)
+\frac{\partial}{\partial y}r\cos\theta\right)\nonumber\\
&=&-\frac{\partial}{\partial x}\sin\theta+\frac{\partial}{\partial y}\cos\theta
\label{par-theta}
\end{eqnarray}
式\eqref{par-r}$\times\cos\theta$-\eqref{par-theta}$\times\sin\theta$より
\begin{equation}
\frac{\partial }{\partial x}=\frac{\partial }{\partial r}\cos\theta-
\frac{\partial }{r\partial\theta}\sin\theta
\label{par-x}
\end{equation}
式\eqref{par-r}$\times\sin\theta$+\eqref{par-theta}$\times\cos\theta$より
\begin{equation}
\frac{\partial }{\partial y}=\frac{\partial }{\partial r}\sin\theta-
\frac{\partial }{r\partial\theta}\cos\theta
\label{par-y}
\end{equation}
式\eqref{vel-x}と微分演算子\eqref{par-x}，\eqref{par-y}より
\begin{eqnarray}
\frac{\partial u}{\partial x}
&=&\left(\frac{\partial}{\partial r}\cos\theta -\frac{\partial}{r\partial\theta}\sin\theta\right)
(v_r\cos\theta-v_{\theta}\sin\theta)\nonumber\\
&=&\frac{\partial v_r}{\partial r}\cos^2\theta
-\frac{\partial v_{\theta}}{\partial r}\cos\theta\sin\theta
-\frac{\partial v_r}{r\partial\theta}\sin\theta\cos\theta
+\frac{v_r}{r}\sin^2\theta
+\frac{\partial v_{\theta}}{r\partial\theta}\sin^2\theta
+\frac{v_\theta}{r\partial\theta}\sin\theta\cos\theta
\label{par-u-x}\\
\frac{\partial v}{\partial y}
&=&\left(\frac{\partial}{\partial r}\sin\theta +\frac{\partial}{r\partial\theta}\cos\theta\right)
(v_r\sin\theta+v_{\theta}\cos\theta)\nonumber\\
&=&\frac{\partial v_r}{\partial r}\sin^2\theta
+\frac{\partial v_{\theta}}{\partial r}\sin\theta\cos\theta
+\frac{\partial v_r}{r\partial\theta}\cos\theta\sin\theta
+\frac{v_r}{r}\cos^2\theta
+\frac{\partial v_{\theta}}{r\partial\theta}\cos^2\theta
-\frac{v_\theta}{r\partial\theta}\cos\theta\sin\theta
\label{par-v-y}
\end{eqnarray}
直角座標の連続の式
\begin{equation}
\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}
+\frac{\partial w}{\partial z}=0
\end{equation}
に，式\eqref{par-u-x}，\eqref{par-v-y}を代入して，極座標における連続の式が得られる．
\begin{equation}
\frac{\partial v_r}{\partial r}+\frac{v_r}{r}
+\frac{1}{r}\frac{v_{\theta}}{\partial\theta}
+\frac{\partial w}{\partial z}
=0
\end{equation}
すなわち
\begin{equation}
\frac{1}{r}\frac{\partial}{\partial r}(rv_r)
+\frac{1}{r}\frac{\partial v_{\theta}}{\partial \theta}
+\frac{\partial w}{\partial z}
=0
\end{equation}