第1章 問題8 解答
$x-y$平面内の二次元流れなので渦度は$z$成分のみである.
流れは軸対称なので,極座標を使うのが便利である.このとき渦度は,式(1.18)にて与えられる.
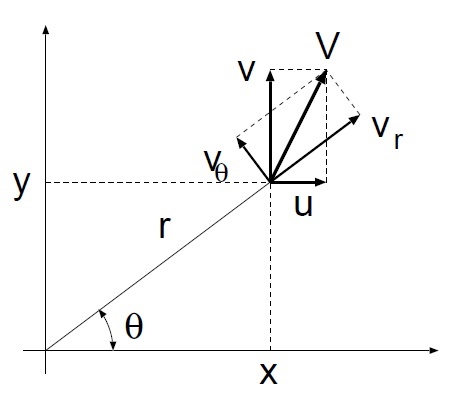
- 円筒座標を使う場合
- $v_r=0$,$v_{\theta}=k/r$を代入して
\begin{equation}
\omega_z=\frac{1}{r}\frac{\partial}{\partial}(rv_{\theta})-\frac{1}{r}\frac{\partial v_r}{\partial \theta}=\frac{1}{r}\frac{\partial}{\partial r}(k)=0
\end{equation}
渦なし流れ
- $v_r=0$,$v_{\theta}=\omega r$を代入して
\begin{equation}
\omega_z=\frac{1}{r}\frac{\partial}{\partial}(rv_{\theta})-\frac{1}{r}\frac{\partial v_r}{\partial \theta}=\frac{1}{r}\frac{\partial}{\partial r}(\omega r^2)=2\omega
\end{equation}
渦あり流れ
- 直角座標を使う場合
\begin{equation}
u=-v_{\theta}\sin\theta,\quad v=v_{\theta}\cos\theta,\quad
\zeta=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}
\end{equation}
- $u=-v_{\theta}\sin\theta=-(k/r)(y/r)=-ky/(x^2+y^2),\quad
v=v_{\theta}\cos\theta=(k/r)(x/r)=kx/(x^2+y^2)$
\begin{eqnarray}
\zeta&=&\frac{\partial}{\partial x}\left(kx/(x^2+y^2)\right)
-\frac{\partial}{\partial y}\left(-ky/(x^2+y^2)\right)
\nonumber\\
&=&k\frac{(x^2+y^2)-2x^2}{(x^2+y^2)^2}
+k\frac{(x^2+y^2)-2y^2}{(x^2+y^2)^2}=0
\end{eqnarray}
渦なし流れ
- $u=-v_{\theta}\sin\theta=-(\omega r)(y/r)=-\omega y,\quad
v=v_{\theta}\cos\theta=(\omega r)(x/r)=\omega x$
\begin{eqnarray}
\zeta&=&\frac{\partial}{\partial x}(\omega x)
-\frac{\partial}{\partial y}(-\omega y)
\nonumber\\
&=&2\omega
\end{eqnarray}
渦あり流れ
