第1章 問題1 解答
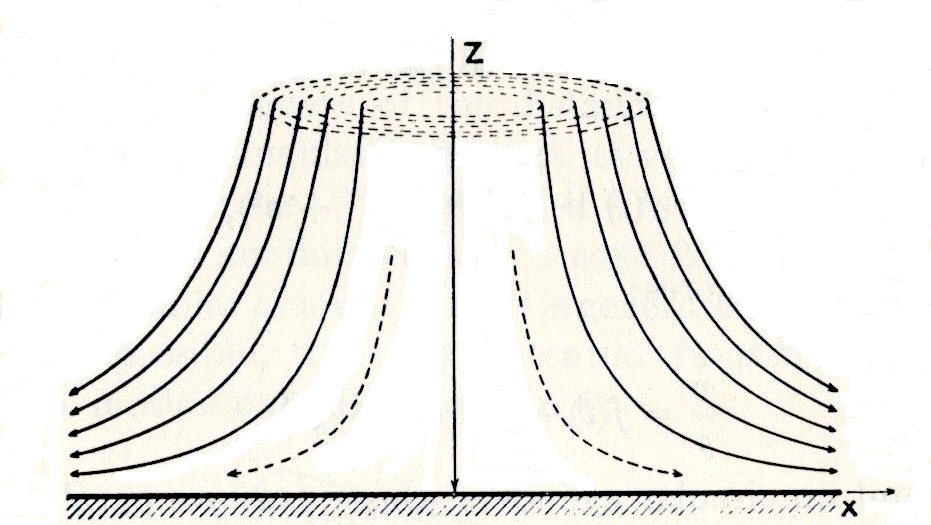
流線の式 \[ \frac{\mbox{d}x}{u}=\frac{\mbox{d}y}{v}=\frac{\mbox{d}z}{w} \] より \[ \frac{\mbox{d}x}{ax}=\frac{\mbox{d}y}{ay} \] $a$を消去し積分すれば \[ \log{x}=\log{y}+\mbox{const.} \rightarrow \log{x/y}=\mbox{const.} \rightarrow{y=Cx} \] これは$\, x-y\, $平面に平行な面で切断した断面では原点を通る直線群となることを示している. 一方,$\, x-z\, $,$\, y-z\, $平面では \[ \frac{\mbox{d}x}{ax}=\frac{\mbox{d}z}{-2az},\qquad \frac{\mbox{d}y}{ay}=\frac{\mbox{d}z}{-2az} \] $a$を消去し積分すれば \[ \log{x}=-\frac{1}{2}\log{z}+\mbox{const.} \rightarrow zx^2=C,\qquad \log{y}=-\frac{1}{2}\log{z}+\mbox{const.} \rightarrow zy^2=C \] 円筒座標$x=r\cos{\theta}$,$y=r\sin{\theta}$,$z=z$を導入すれば, \[ zr^2=C, \mbox{or}\,\quad z=\frac{C}{r^2} \] と表される.流線を立体的に描けば下図のようになり,$\, z\, $軸を中心とする軸対称流れになる.
