第1章 問題10 解答

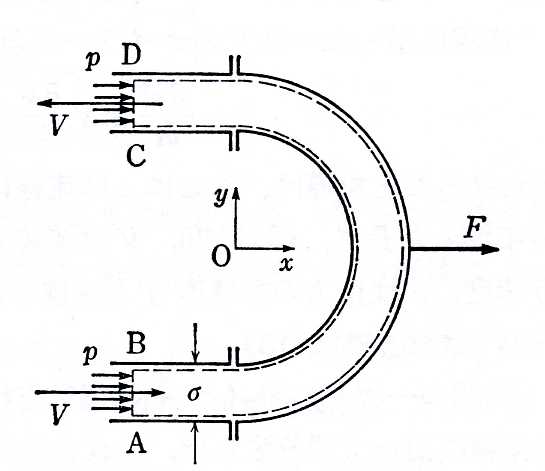
運動量の法則，テキストの式(1.55)，(1.56)および(1.57)より \begin{equation} \rho \int u\mbox{d}Q=P_x-R_x, \quad \rho \int v\mbox{d}Q=P_y-R_y \label{eq:momentum} \end{equation} ここに$\rho\int u\mbox{d}Q$，$\rho\int v\mbox{d}Q$はそれぞれ単位時間に検査面から流出する運動量の$x$，$y$方向成分で，流出が正，流入が負と定義されている．また，$P$は検査面に働く圧力が流体に作用する力，$R$は検査面内の物体が流体から受ける力で，添え字$x$，$y$はそれぞれ$x$，$y$方向の成分を示している．

面AB，CDの面積は等しいので速度の大きさは等しく，ベルヌーイの式より圧力も等しい． 本問では，$P$は面ABおよびCDに作用する力である． \begin{equation} P_x=p\sigma|_{AB} + p\sigma|_{CD}=2p\sigma,\quad P_y=0 \end{equation}

運動量の流出は \begin{equation} \rho\int u\mbox{d}Q=\rho V\sigma(-V)-\rho V\sigma V=-2\rho\sigma V^2,\quad \rho\int v\mbox{d}Q=0 \end{equation}

式\eqref{eq:momentum}より \begin{eqnarray} R_x&=&P_x-\rho \int u\mbox{d}Q=2\sigma(p+\rho V^2)\\ R_y&=&0 \end{eqnarray}