第4章 問題
- 渦度$\omega$の$x$, $y$, $z$方向の成分を$\xi$, $\eta$, $\zeta$
とするとき次の式が成立することを示せ.
解答
\[
\frac{\partial\xi}{\partial x}+
\frac{\partial\eta}{\partial y}+
\frac{\partial\zeta}{\partial z}=0
\]
- 半径$a$, 単位長さあたりの強さ$\varGamma$の渦輪の中心を通り,渦輪
に垂直な直線上で,渦輪から距離$x$の誘導速度を求めよ(図4.14).
解答
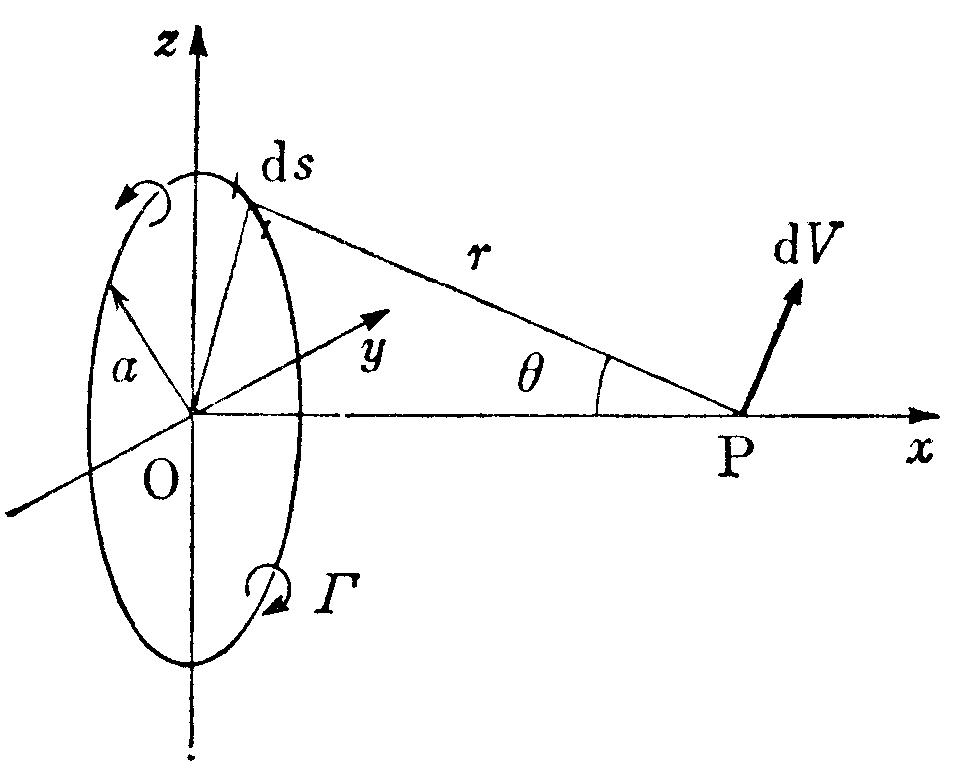 図4.14:渦 輪
図4.14:渦 輪
- 点$\mathrm{A}(-a,0)$に強さ$\varGamma$の直線状渦糸が,点
$\mathrm{B}(a,0)$に強さ$-\varGamma$の直線状渦糸ある.等ポテンシャ
ル線および流線はいずれも円群で与えられること,および線分
$\overline{\mathrm{AB}}$の垂直二等分線は流線となることを示せ(図4.15).
解答
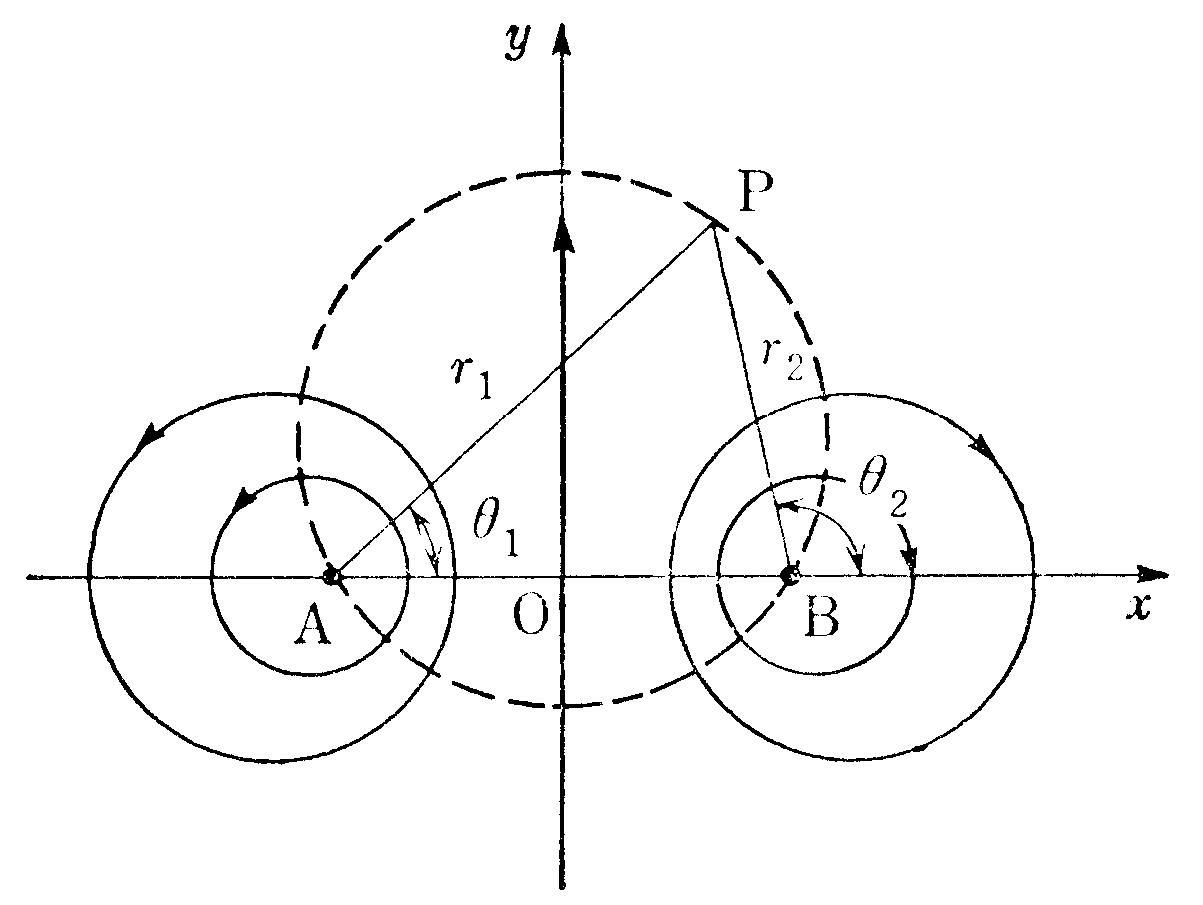 図415 渦 対
図415 渦 対
- 直線壁から距離$h$の位置に強さ$\varGamma$の直線状渦糸がある.渦糸
の運動を説明せよ.
解答
- 無限に広い静止流体中に,原点を中心とする半径$a$の円があり,その外
部の点$\mathrm{A}(l,0)$に直線状渦糸が,鏡像の点
$\mathrm{B}(a^2/l,0)$に強さ$-\varGamma$の直線状渦糸がある.
- 上記の円は流線となることを示せ.
- 前記の円が固体境界のとき,円の内部渦糸Bの運動を説明せよ.
- 前記の円が固体境界であって,そのまわりに強さ$\, \varGamma^\prime\, $
の循環があるとき,円の外の渦糸Aの運動を説
明せよ(図4.16).
解答
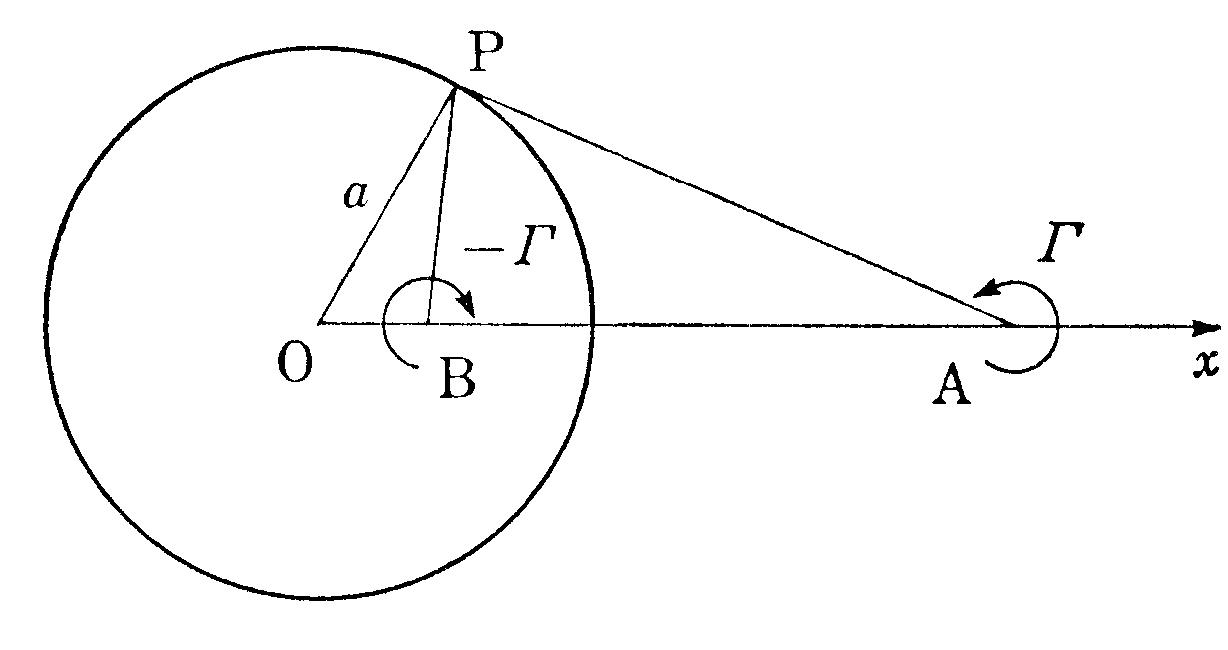 図4.16 円の鏡像
図4.16 円の鏡像
- $z$平面上の点$\mathrm{A}(-a,0)$に強さ$\varGamma$の直線状渦糸が,
$\mathrm{B}(a,0)$に強さ$-\varGamma$の直線状渦糸が固定されている.
いま$y$軸の負の方向に速度$V$の一様流が加えられたとき,$y$軸上によ
どみ点が存在するための条件を求めよ.また,よどみ点が存在するとき
その座標を求め,よどみ点を通る流線の式を求めよ(図4.17).
解答
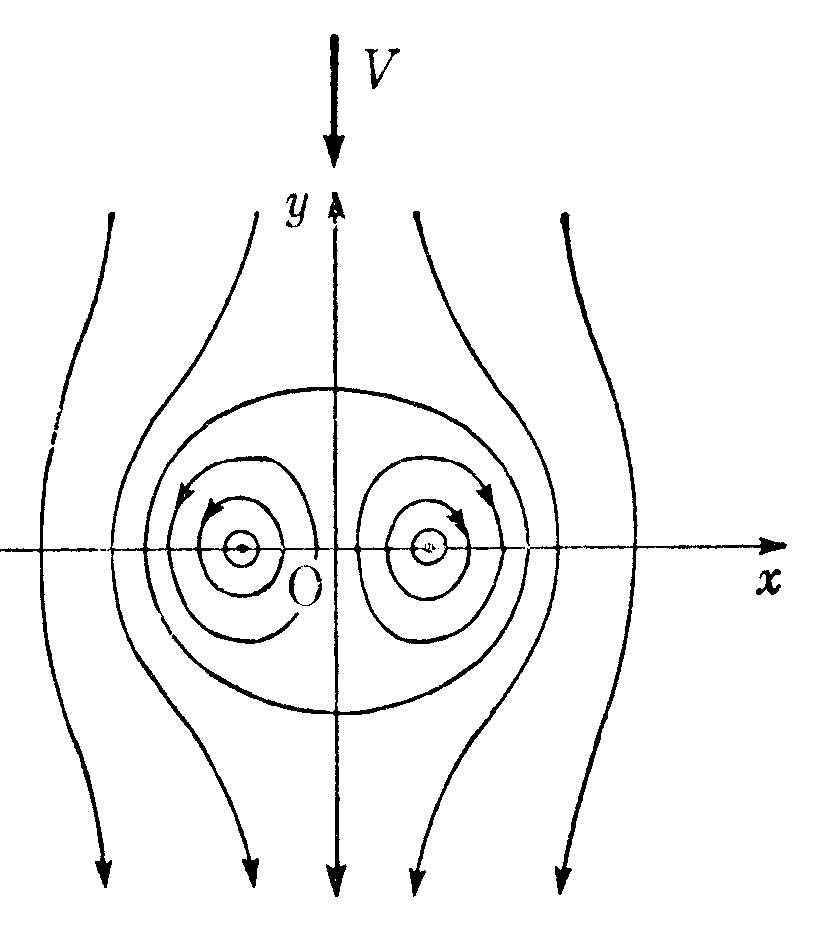 図4.17 一様流中の渦対
図4.17 一様流中の渦対
- 無限に広い静止流体中に,強さ$\varGamma_k(k=1, 2, \dots, n)$の$n$
個の直線状渦糸がそれぞれ点$(x_k, y_k)$に存在するとき,$j$番目の渦
糸の運動方程式は
\[
u_j\left(=\frac{d x_j}{d t}\right)
=-\frac{1}{2\pi}\sum_{k=1,\, k\ne j}^{n}\frac{\varGamma(y_j-y_k)}{r_{kj}^2}
,\quad
v_j\left(=\frac{d y_j}{d t}\right)
=\frac{1}{2\pi}\sum_{k=1,\, k\ne j}^{n}\frac{\varGamma(x_j-x_k)}{r_{kj}^2}
\]
で与えられることを示せ.ただし,
$r_{kj}=[(x_k-x_j)^2+(y_k-y_j)^2]^{1/2}$.
解答
- 直交する二つの直線壁$x=0$,$y=0$で囲まれた$x\ge0$,$y\ge0$なる領
域に,強さ$\varGamma$の直線状渦糸がある.渦糸に誘導される速度成分
を求めよ.つぎにこの渦糸は
\[
\frac{1}{x^2}+\frac{1}{y^2}=\text{const.}
\]
で表される経路に沿って動くことを示せ(図4.18).
解答
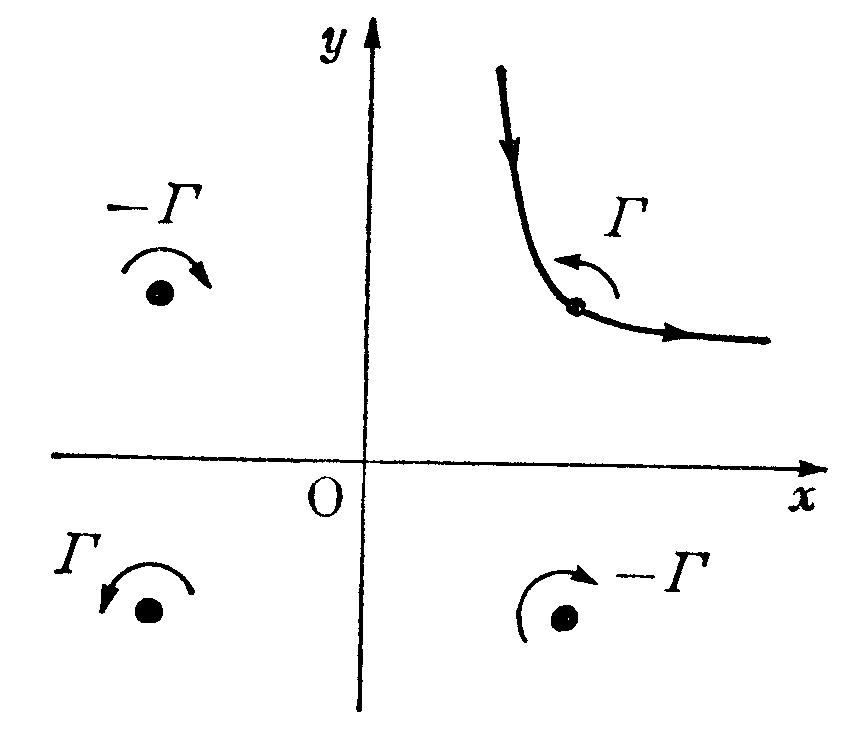 図4.18 直角をなす二つの直線壁間の渦糸の運動
図4.18 直角をなす二つの直線壁間の渦糸の運動
- 風のある日に直径2mmの送電線が振動している音を発生している.風速
$10$m/sであるとし,振動の周波数を求めよ.ただし空気の動粘度
$15\times10^{-6}\mathrm{m}^2/s$($20^\circ\mathrm{C}$)とする.
解答
- 強風下で旗がはためく理由を定性的に説明せよ.
解答









