第4章 問題8 解答

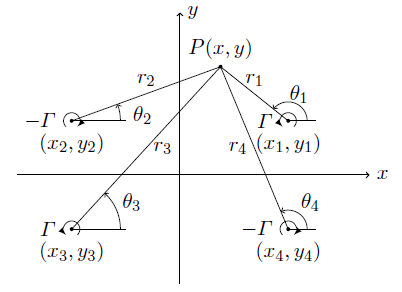
直交する直線壁に囲まれた点$\, (x_1, y_1)\, $にある渦糸の鏡像位置は， \begin{equation} \left. \begin{array}{r@{=}l} \mbox{第2象限：}&(x_2,y_2)=(-x_1,y_1)\\ \mbox{第3象限：}&(x_3,y_3)=(-x_1,-y_1)\\ \mbox{第4象限：}&(x_4,y_4)=(x_1,-y_1) \end{array} \right\} \end{equation} これらの渦糸の複素速度ポテンシャル$\, W\, $は， \begin{eqnarray} W&=&-\frac{i\varGamma}{2\pi}\log(z-z_1) +\frac{i\varGamma}{2\pi}\log(z-z_2) -\frac{i\varGamma}{2\pi}\log(z-z_3) +\frac{i\varGamma}{2\pi}\log(z-z_4)\\ &=&-\frac{i\varGamma}{2\pi}\log\left(r_1e^{i\theta_1}\right) +\frac{i\varGamma}{2\pi}\log\left(r_2e^{i\theta_2}\right) -\frac{i\varGamma}{2\pi}\log\left(r_3e^{i\theta_3}\right) +\frac{i\varGamma}{2\pi}\log\left(r_4e^{i\theta_4}\right)\nonumber\\ &=& \frac{\varGamma}{2\pi}(\theta_1-\theta_2+\theta_3-\theta_4) -i\frac{\varGamma}{2\pi}\log\left(\frac{r_1r_3}{r_2r_4}\right) \end{eqnarray} 複素速度ポテンシャル$\, W\, $の実部は速度ポテンシャル$\, \varPhi\, $，虚部は流れ関数$\, \varPsi\, $である．$\, x\, $軸上では$\, r_1/r_4=1\, $，$\, r_3/r_2=1\, $であるから，$\, \varPsi=0\, $，$\, y\, $軸上では$\, r_1/r_2=1\, $，$\, r_3/r_4=1\, $であるから，$\, \varPsi=0\, $．したがって，この流れは直交する直線壁の流れを表していることが確認できる．

渦糸は自分自身に速度を誘起しないから，それを含まない複素速度ポテンシャルを$\, W^\prime\, $と表せば，渦糸の速度$\, (u_1, v_1)\, $は \begin{eqnarray} u_1-iv_1=\frac{\mbox{d}W^\prime}{\mbox{d}z}\Bigg|_{z=z_1} &=& \frac{i\varGamma}{2\pi}\frac{1}{z_1-z_2} -\frac{i\varGamma}{2\pi}\frac{1}{z_1-z_3} +\frac{i\varGamma}{2\pi}\frac{1}{z_1-z_4}\nonumber\\ &=&\frac{i\varGamma}{4\pi}\left(\frac{1}{x_1}-\frac{1}{x_1+iy_1} +\frac{1}{iy_1}\right) =\frac{i\varGamma}{4\pi}\left( \frac{1}{x_1}-\frac{x_1-iy_1}{x_1^2+y_1^2}-\frac{i}{y_1} \right)\nonumber\\ &=&\frac{\varGamma}{4\pi}\left( \frac{1}{y_1}-\frac{y_1}{x_1^2+y_1^2}\right) +i\frac{\varGamma}{4\pi}\left( \frac{1}{x_1}-\frac{x_1}{x_1^2+y_1^2}\right) \end{eqnarray} ゆえに， \begin{equation} u_1=\frac{\mbox{d}x_1}{\mbox{d}t} =\frac{\varGamma}{4\pi}\left(\frac{1}{y_1}-\frac{y_1}{x_1^2+y_1^2}\right) ,\quad v_1=\frac{\mbox{d}y_1}{\mbox{d}t} =\frac{\varGamma}{4\pi}\left(-\frac{1}{x_1}+\frac{x_1}{x_1^2+y_1^2}\right) \end{equation} 上式を積分することにより渦糸の経路が求められる．その経路の傾きは \begin{equation} \frac{\mbox{d}y_1}{\mbox{d}x_1} =\frac{\varGamma}{4\pi}\left(-\frac{1}{x_1}+\frac{x_1}{x_1^2+y_1^2}\right)\bigg/ \frac{\varGamma}{4\pi}\left(\frac{1}{y_1}-\frac{y_1}{x_1^2+y_1^2}\right) =-\frac{y_1^3}{x_1^3} \end{equation} すなわち， \begin{equation} \frac{\mbox{d}x_1}{x_1^3}+\frac{\mbox{d}y_1}{y_1^3}=0 \end{equation} これを積分して， \begin{equation} \frac{1}{x_1^2}+\frac{1}{y_1^2}=\mbox{const.}\qquad \mbox{or}\qquad \frac{1}{x^2}+\frac{1}{y^2}=\mbox{const.} \end{equation}