第4章 問題3 解答
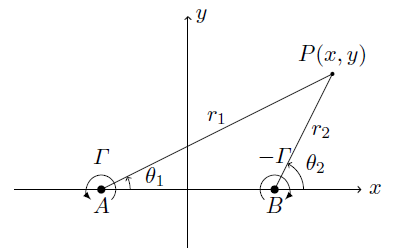
複素速度ポテンシャルは,式(3.30)より
\begin{eqnarray}
W&=&-\frac{i\varGamma}{2\pi}\log(z+a)+\frac{i\varGamma}{2\pi}\log(z-a)
\nonumber\\
&=&-\frac{i\varGamma}{2\pi}(\log r_1+i\theta_1)
+\frac{i\varGamma}{2\pi}(\log r_2+i\theta_2)
\nonumber\\
&=&-\frac{i\varGamma}{2\pi}\log\left(\frac{r_1}{r_2}\right)
+\frac{\varGamma}{2\pi}(\theta_1-\theta_2)
\end{eqnarray}
複素速度ポテンシャルの実部は速度ポテンシャル$\, \varPhi\, $,虚部は流れ関数$\, \varPsi\, $であるから,
\begin{eqnarray}
\varPhi&=&\frac{\varGamma}{2\pi}(\theta_1-\theta_2)\label{eq:ptn}\\
\varPsi&=&\frac{\varGamma}{2\pi}\log\left(\frac{r_1}{r_2}\right)
\label{eq:str}
\end{eqnarray}
-
等速度ポテンシャル線について考える.図を参考にして,
\begin{equation}
\theta_1=\tan^{-1}\left(\frac{y}{x+a}\right),\quad
\theta_2=\tan^{-1}\left(\frac{y}{x-a}\right)
\end{equation}
ここで,三角関数の和の公式
\begin{equation}
A-B=\tan^{-1}\left(\frac{\tan A-\tan B}{1+\tan A \tan B}\right)
\end{equation}
を用いれば,
\begin{eqnarray}
\theta_1-\theta_2&=&\tan^{-1}\left(\frac{y/(x+a)-y/(x-a)}
{1+y/(x+a)\cdot y/(x-a)}\right)
=\tan^{-1}\left(\frac{xy-ay-(xy+ay)}{x^2-a^2+y^2}\right)\nonumber\\
&=&\tan^{-1}\left(\frac{-2ay}{x^2+y^2-a^2}\right)
\end{eqnarray}
等速度ポテンシャル線は$\, \varPhi=\mbox{const.}\, $より
\begin{equation}
\frac{-2ay}{x^2+y^2-a^2}=C
\end{equation}
整理して,
\begin{equation}
x^2+\left(y+\frac{a}{C}\right)^2=a^2\left(1+\frac{a^2}{C^2}\right)
\end{equation}
これは,円の中心が$\, (0, -a/C)\, $,半径$\, a\sqrt{1+a^2/C^2}\, $の円群である.
- 流線について考える.流れ関数が一定の曲線であるから,
\begin{equation}
\frac{r_1}{r_2}=C,\quad \frac{(x-a)^2+y^2}{(x+a)^2+y^2}=C^2
\end{equation}
\[
x^2-2ax+a^2y^2=C^2(x^2+2ax+a^2y^2)\\
(1-C^2)x^2-2a(1+C^2)x+(1-C^2)y^2+a^2(1-C^2)=0\\
x^2-2a\frac{1+C^2}{1-C^2}x+y^2+a^2=\left(x-a\frac{1+C^2}{1-C^2}\right)^2+y^2+a^2-a^2\left(\frac{1+C^2}{1-C^2}\right)^2=0
\]
ゆえに,
\begin{equation}
\left(x-a\frac{1+C^2}{1-C^2}\right)^2+y^2=a^2\left\{\left(\frac{1+C^2}{1-C^2}\right)^2-1\right\}
\end{equation}
これは,中心が$\, (a(1+C^2)/(1-C^2),\, 0)\, $,半径$\, a\sqrt{\{(1+C^2)/(1-C^2)\}^2-1}\, $の円である.
