
| 
| 
|
結論的にいうと、等時間通過説は間違えています。ここでは、等角写像法を用いてジューコフスキー翼まわりの流れを解析することにより、等時間通過説を検証することにします。
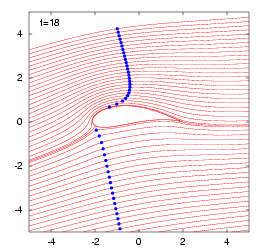
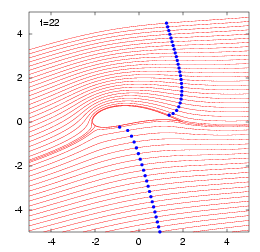
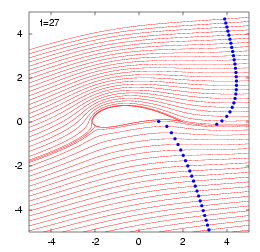
特に、円弧翼の場合でかつ迎え角\(0^\circ\)の場合は、翼面上に淀み点がないので、流体粒子が前縁から後縁に到達するに要する時間は有限の大きさになります。そこで、流体粒子が翼上面、下面を通過する時差を解析的に求めます。まずは、円弧翼とジューコフスキー翼を過ぎる流れのタイムラインをアニメーションで見て下さい。 Click Here!
さて、翼に揚力が発生する仕組みは、多くの人々の関心の引き付けることから、インターネット上には様々な解説があります。また、多くの解説本も出版されています。そこでの主たる論調は、
従来の説明「翼は上方に反っており、翼の上面は下面よりも長いので、翼の前縁で分かれた流体粒子が後縁で同時に到着するためには、上面側の流体粒子の速度は下面よりも早くなければならない。したがって、ベルヌーイの定理から上面の方が下面よりも圧力が低くなり、揚力が発生する」(等時間通過説、Equal Transit Theory)は、流体粒子が後縁で同時に到着しなければならないという必然性はないのだから間違いである。というものです。
確かに、翼の前縁で上面と下面に分かれた流体粒子が翼の後縁で同時に到着する必然性はありませから、等時間通過説は間違えています。上面の方が下面よりも早く後縁に達するという記述は、例えば、以下のようなものです。
Experimental results and computational fluid dyanamic calculations clearly show that a fluid element moving over the top surface of an airfoil leaves the trailing edge long before its companion element moving over the bottom surface arrives at the trailing edge.
風洞という、空気の流れをつくる実験装置のなかで、煙を流して気流の様子を観察すると、たいてい、上面の流れのほうが早く流れる様子が観測できる。
"It is often said that the lift on a wing is generated because the flow moving over the top surface has a longer distance to travel and therefore needs to go faster. This common explanation is actually wrong." Here, aerodynamics expert Professor Holger Babinsky from the University of Cambridge's Department of Engineering debunks a popular, yet misleading, explanation of how wings lift. For more information, read the accompanying story published by the University of Cambridge
しかし、残念ながら、翼の上面と下面に分かれた流体粒子が後縁に到達する「時差」を定量的に示した解説はないように思われます。その原因として考えられるのは、翼の前縁近傍の澱み点では、流速が\(0\)となるので翼の表面に沿っう流体粒子の追跡ができないことです。一方、実験では、翼表面に境界層ができるので、境界層の外側を流れる流体粒子を可視化していることになるからです。
そこで、筆者はJoukowski翼を過ぎる流れを等角写像法で解析し、ルンゲ・クッタ法で流体粒子を追跡してみました。ただ、澱み点を通る岐点流線上では、前述の理由から追跡できないので、そこからわずかにずらした流線上で追跡します。これを流れの可視化法で知られるタイムライン法と同じように表示しています。さらに、円弧翼が迎え角が\(0^\circ\)のとき、澱み点がないことに注目して、次節に示すように流体粒子の通過時間の差(時差)を解析的に求めています。詳細は、
菊地正憲「翼を通過する流体粒子の追跡-等時間通過説の検証-」『可視化情報』(2015.1 Vol.35 No. 136 pp. 25-28.)
をご一読ください。
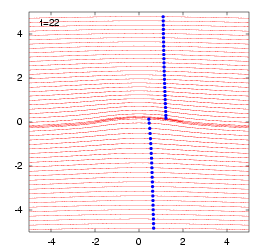
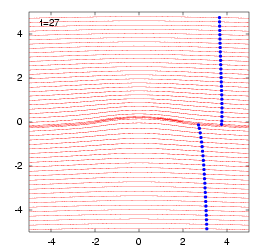
アニメーション結果を見るには、このページトップのClick Hereをクリックしてみてください。ただし、等角写像法でアニメーションを作成する際に注意すべきことは、写像面と物理面で対応する2点間を過ぎるに要する時間が場所により異なることです。このことは、迎え角が\(0^\circ\)の平板を過ぎる流れを考えればすぐにわかります。物理面では平板が流れを乱すことがありませんから、流体粒子はどの位置においても同じ速度で通過していきます。一方、写像面では円柱まわりの流れになるので、円柱表面上に澱み点が現れ、澱み点を通る流線上では、いつまでたっても流体粒子が円柱に到達することはないからです。 図解を見る!
写像面と物理面で対応する2点間を過ぎるに要する時間が場所により異なることは以下のようにして示すことができます。写像関数を \begin{align} z=\zeta+\frac{a^2}{\zeta} \end{align} とすると、物理面(\(z\)平面)と写像面(\(\zeta\)平面)において対応する 2点間\(|dz|\)、\(|d\zeta|\)を移動するに要する時間\(|dz|/q_z\)、 \(|d\zeta|/q_\zeta\)には次式の関係が成立します。 \begin{align} \frac{|dz|}{q_z}=|f^\prime(\zeta)|^2\frac{|d\zeta|}{q_\zeta} \end{align} ここに、\(q_z\)、\(q_\zeta\)はそれぞれの面における速度の大きさで、両者には \begin{align} q_z=\frac{q_\zeta}{|f^\prime(\zeta)|} \end{align} の関係があります。
| 
| 
|
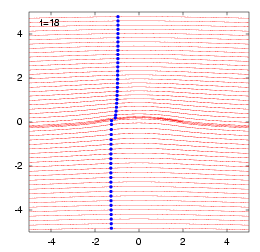
円弧翼が迎え角が\(0^\circ\)の一様流中にあるときは、無衝突流れ、すなわち、上図のように澱み点のない流れとなります。この時は、翼の上面と下面に分かれた流体粒子が後縁を通過する時間を解析的に計算することができます。以下にそれを示します。
円弧翼の弦長を\(C\)、反りを\(h\) とし、反り比\(h/C\)及び迎え角\(\alpha\)が小さいときは、翼上下面における速度\(W_C\) の線形近似は次式にて与えられます。
\begin{align} W_C=W_\infty\left[1\pm4\frac{h}{C}\sqrt{1-4\left(\frac{x}{C}\right)^2} \pm\alpha\sqrt{\frac{1-2x/C}{1+2x/C}}\, \right] \label{W_C} \end{align}ここに、\(W_\infty\)は主流速度、\(x\)は翼弦に沿う座標で、前縁は\(x=-C/2\)、後縁は\(x=C/2\)です。式\eqref{W_C}の第1項は一様流を、第2項は翼の反り、第3項は迎え角の効果を表わしています。
この式は、以下の本の等角写像法を扱った章の47頁にあります。
Schlichting. H., Truckenbrodt. E. A. 『Aerodynamics of the Airplane』(McGraw-HILL, 1979)
これと等価な式は、以下の本の薄翼近似を扱った節の220頁にあります。
今井功『流体力学(前編)』(第3版、裳華房、1975)
迎え角\(\alpha\)が\(0^\circ\)のとき、流体粒子が翼の上面、下面に沿って前縁から後縁まで移動するに要する時間をそれぞれ、\(T_\pm\)とすれば \begin{align} T_{\pm}=\int_{-C/2}^{C/2}\frac{dx}{W_C} =\frac{C}{W_\infty}\left[1 \mp \pi \frac{h}{C} \right] \end{align} ただし、反り比の二次以上の微小量は省略しています。これより、迎え角が\(0^\circ\)の円弧翼の場合、前縁で上面側と下面側に分かれた流体粒子が後縁に到達する時間には、以下の時差\((T_--T_+)\)があることになります。この流れの代表時間\(C/W_\infty\)で無次元化すれば \begin{align} \frac{W_\infty(T_- - T_+)}{C}=2\pi\frac{h}{C} \label{時差} \end{align} となり、無次元の時差は、線形近似では反り比に比例することが分かります。
翼から十分下流側では流速は主流の\(W_\infty\)となるので、式\eqref{時差}は、ズレ量の無次元表示と見なすことができます。この考えに基づいて、アニメーション図で、\(t=38\)のときのズレ量を測りました。反り比が\(0.05\)のとき、アニメーションからは約\(0.286\)、近似式\eqref{時差}からは\(0.314\)が得られました。
注
菊地 正憲